Rerunning simulation such that output is identical

Advanced Features and User Routines
1

Dear FLUKA experts,

Question: Is there a way to rerun a simulation such that the output is identical (e.g. by forcing the random seed to a preset value)?

More info: I am investigating how different settings along the beamline may influence the radiation downstream, while keeping the settings identical upstream. To reduce possible sources of inconsistencies from statistics, I would like to run the simulation with the same initial seed such that the radiation before my changes is identical and it only changes when I also change the settings, thereby isolating the impact/consequences of the changes I make.

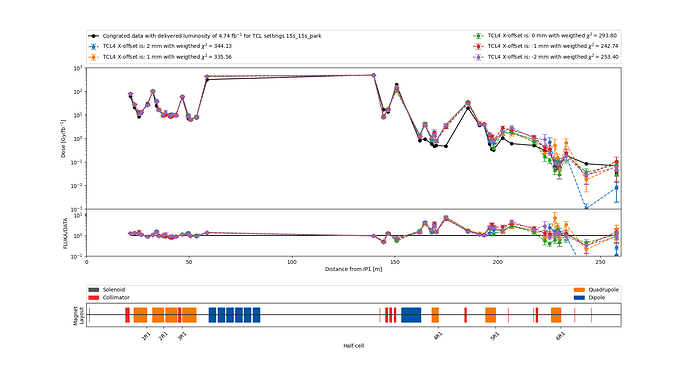
For example, look at the graph below, where I run a simulation with just one difference in the settings at ~150 m for 5 different values. Therefore, I would have expected (wished for) identical (and I truly mean identical, not just in agreement with each other) results before 150 m and changes only afterwards.

Each of these 5 different simulations were run on a cluster with 50 jobs, where the seed was set from N=1 to 50
RANDOMIZ 1.0 N.0
with 20 cycles and 100 primaries each.

tcl4_offset_study_errobars_50000primaries
tcl4_offset_study_errobars_50000primaries1848×982 138 KB

Is such a procedure possible, are there counter-arguments against it?

Thank you so much for your time!

Best,
Daniel

2

Repeating the same random sequence - which is possible - makes sense only for code debugging purposes.
For production purposes, you can expect truly identical results for identical problems only after an infinite number of primaries, which is not a real possibility. The results variation reflects their statistical uncertainty, implying that you cannot take the results of a single batch as the ‘true’ ones to compare with.
Moreover, even starting from the same random seed, if you alter any ingredient of your problem (as geometry settings), the random sequence will be immediately modified as soon as a particle is affected by your change, e.g. in the very first history. But this does not mean at all that the consequent variation in the results is physically due to your modification (thereby it will not allow you to isolate the impact/consequences of the changes you made), rather that your statistics gets different.
In short, in order to appreciate a true difference between different settings, you have to achieve the required accuracy (i.e. statistical uncertainty minimization) for both configurations.

1 Like