Dose deposition by 3 MeV alphas lower than expected

[lpalenciano (Lidia Palenciano Castro)]

Dear FLUKA experts,

I am trying to score dose deposition in a water sphere when a monoenergetic, point alpha-particle source is placed at its center, for energies between 3 and 8 MeV. I am comparing the FLUKA results with those obtained using the Monte Carlo code PENHAN.

In most cases, I observed percentage variations of around 2-3% between the two codes, calculated as:
variation = ((value_PENHAN - value_FLUKA)/value_FLUKA)*100

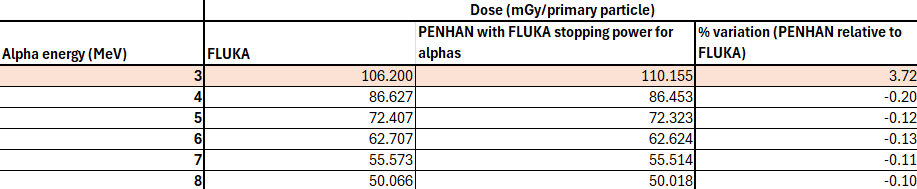
I assume that these differences, besides the different simulations approaches and physics models, are related to differences in the alpha stopping powers in water used in each code. However, as shown in the attached table (‘table.png’), I obtained a significantly larger discrepancy (around 6%) for 3 MeV alpha particles, while differences in the stopping power for these lower energies are not that much.

To investigate this issue for 3 Mev alphas, I conducted three FLUKA simulations:

• In Simulation 1 I set the electron transport energy cutoff to 1 keV (via EMFCUT card) and the delta-ray production cutoff to 1 keV (via DELTARAY card). This gave me the already reported results.
• In Simulation 2 I increased the delta-ray production cutoff to 10 keV, so no secondary electrons are produced due to the low energy of the alphas. I would expect to obtain a similar result, since in Simulation 1 the produced electrons have very low energies and therefore should deposit their energy close to their production sites. Nevertheless, in Simulation 2 I obtained a higher dose, ~110 mGy, closer to PENHAN’s result.
• In Simulation 3, I maintained the delta-ray production cutoff in 1 keV and increased the electron transport energy cutoff to 100 keV. With this all generated electrons should deposit their energies in the production site. Here I obtained a similar dose than in Simulation 1.

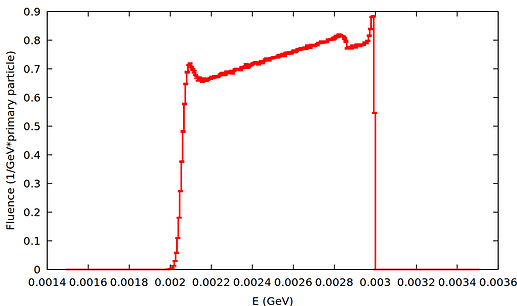
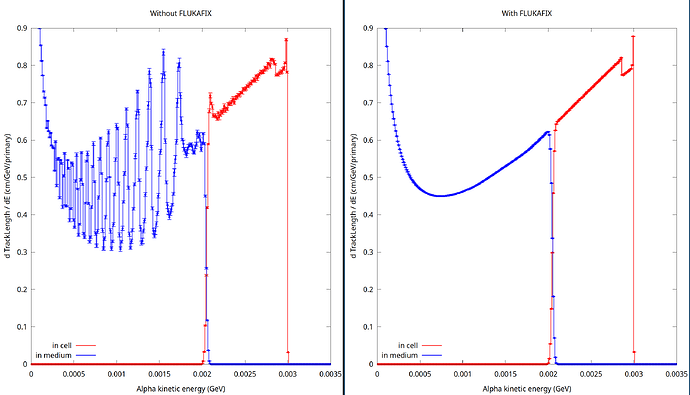
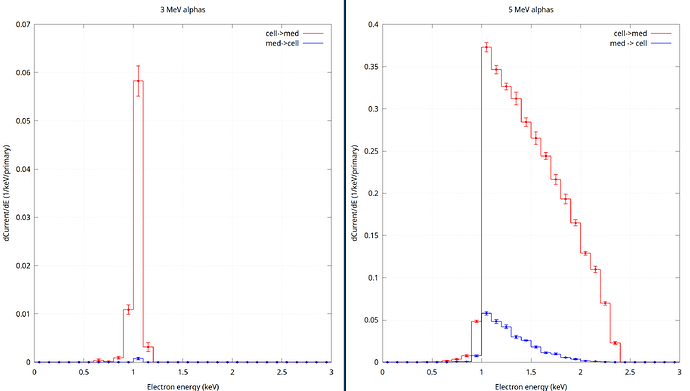
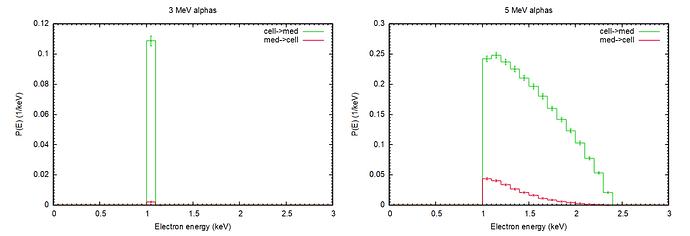
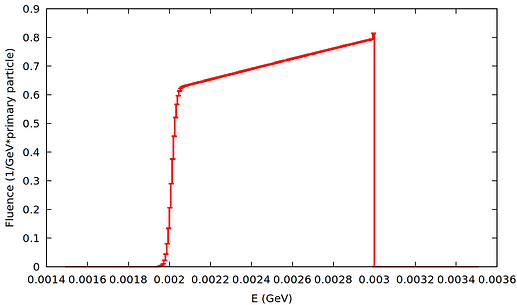
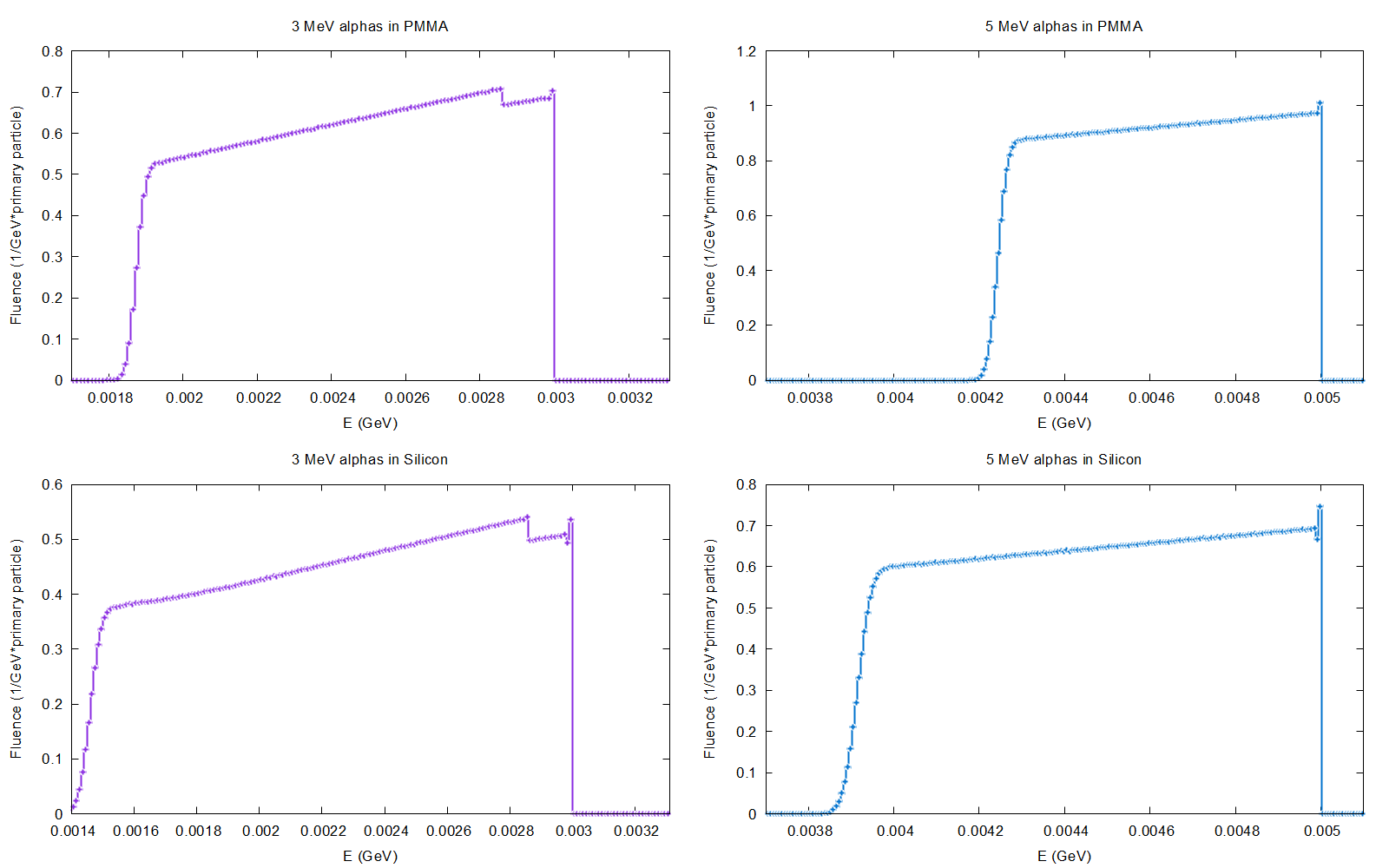
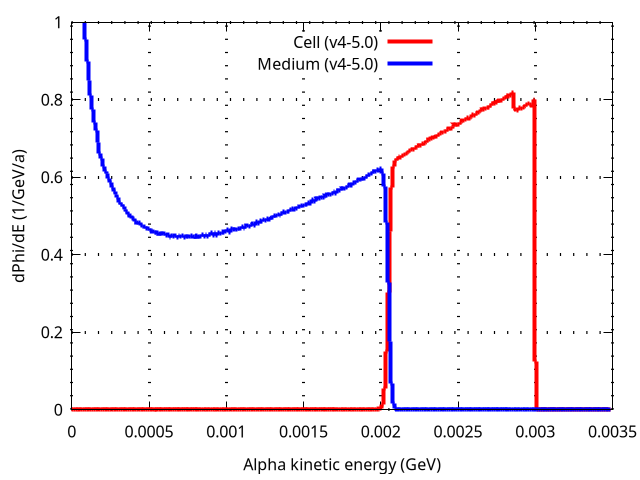
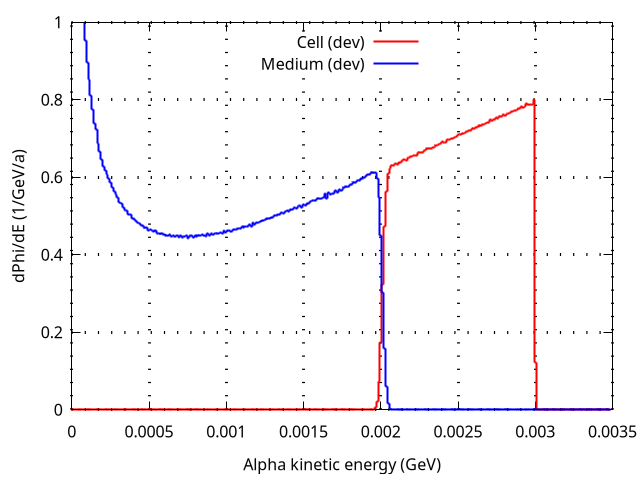
Additionally, I analyzed the alpha and electron fluences within the sphere using a USRTRACK card in Simulation 1. For 3 MeV alphas, the fluence distribution seems to show an unusual behavior compared to higher energy cases. I attach the corresponding graphs for 3 and 5 MeV (fluence_3_mev.png and fluence_5_mev.png).

Could you help me understand these results for 3 MeV alphas? Specifically:

• Why does the fluence distribution show that unexpected behavior?
• Where is the missing energy going, leading to such a low deposited dose?

I attach the input files for the three simulations mentioned:

• alpha_1.inp (Simulation 1, i.e, both transport and delta-ray production cutoffs set to 1 keV)
• alpha_2.inp (Simulation 2, i.e., transport cutoff at 1 keV and delta-ray production cutoff at 10 keV)
• alpha_3.inp (Simulation 3, i.e., transport cutoff at 100 keV and delta-ray production cutoff at 1 keV).

alpha_1.inp (2.3 KB)
alpha_2.inp (2.4 KB)
alpha_3.inp (2.4 KB)

Thank you very much in advance for your help!

Best regards,
Lidia

[cesc (Francesc Salvat Pujol)]

Dear Lidia,

Apologies for the delay.

For the 3-MeV case we acknowledge an artifact in the energy-differential fluence of alpha particles.

The low-energy end of it and the wiggly behavior can however be mitigated. For completeness in the plots below you see the energy-differential tracklength distribution in the R=7\ \mu\textrm{m} sphere (in red, what you already show) and in the surrounding water (in blue). The plot to the left is your original situation, which magnifies into substantial artifacts in the surrounding water. These are effectively smoothed out by passing a FLUKAFIX card requesting a maximum fractional energy loss of 0.001 (i.e. 0.1%) in water (i did not fine-tune this, maybe a less stringent value is sufficient).

There remains however the step-like artifact right below 3 MeV, which warrants further examination in the future on our side.

The dose itself remains essentially unaltered under the inclusion of the FLUKAFIX card. The higher dose you observe with PENHAN compared to FLUKA, beyond what you’d expect from the slightly higher stopping powers in PENHAN than in FLUKA, might be due to these codes’ different e- transport treatment and especially their different transport limits: down to 1 keV for FLUKA, down to 100 eV for PENELOPE-based codes.

For reference below, i note here the energies of the delta rays produced in the sphere in both cases:

• 3 MeV alpha isotropic beam → 2-3 MeV alphas in the sphere → 1.1 to 1.6 keV delta rays produced in the sphere
• 5 MeV alpha isotropic beam → 4.3-5 MeV alphas in the sphere → 2.4 to 2.7 keV delta rays produced in the sphere

I note also from NIST ESTAR that the range of 10 keV e- (the lowest ESTAR goes) in water is ~2.5 um. Thus, e- that manage to make it from the sphere into the surrounding water are produced in the outermost few 100 nm of the sphere.

The plot below to the right shows the e- current from the cell (7-um sphere) to the surrounding water (med) in red, while the blue curve represents the current back into the cell from the surrounding medium for the 5-MeV alpha case (at this somewhat higher energy you can legitimately have e- produced in the surrounding medium penetrating the sphere). So far so good: delta rays make it back into the sphere. Instead, for the 3-MeV alpha case (left plot), delta rays are produced almost exclusively in the sphere; some of them traverse into the surrounding water, and only a small current makes it back into the sphere:

This is at odds with the expectation that e- backscattering normally increases at low energies. See, e.g., this figure from a nice e- transport reference

This behavior is a consequence of FLUKA’s 1 keV lower transport limit for e-: those e- that make it into the surrounding water typically drop below transport threshold and deposit their energy there. Instead, physically, their history would carry on and some of them would even scatter back into the small sphere (!). Indeed, for low-energy e- the differential cross section for elastic scattering (anyway quite intensive - e- trajectories are in themselves quite corrugated) in water actually increases and exhibits an enhanced backscattering towards lower energies and especially when the energy drops towards 100 eV:

Instead, I surmise that in PENHAN e- produced in the sphere in the 3-MeV alpha case have a significant chance to backscatter into the sphere and deposit more of their energy in it as their histories are followed down to 100 eV, hence the higher dose you obtain with PENHAN.

The above Gedankenexperiment also provides a tentative explanation for getting results similar to PENHAN when you rose the production cutoff to 10 keV in FLUKA: you effectively forced deposited in the sphere the energy carried away by delta rays which would ultimately healthily bounce back into the sphere.

Hope this helps somewhat. If you meanwhile have additional ingredients to clarify/adapt the picture, feel free.

Cheers,

Cesc

[lpalenciano (Lidia Palenciano Castro)]

Dear Cesc,

Thank you very much for your response.

Now I see how using the FLUKAFIX card the other artifacts disappear; this is equivalent to reducing the maximum path step via the STEPSIZE card, right?

Nevertheless, I am still concerned about the one just below 3 MeV, as I suspect it is related to the lower doses I obtain with 3 MeV alpha particles.

Regarding your comment on electron transport, although PENHAN allows setting the transport energy cutoff down to 100 eV, in my simulations I set this cutoff to 1 keV - just as in FLUKA - to ensure the most comparable results between both codes. In addition, in PENHAN, I also set the parameter controlling the generation of secondary electrons by hadrons (in some way analogue to the DELTARAY card in FLUKA) to 1 keV. Threrefore, just as you mentioned for FLUKA, in PENHAN, delta-rays produced by 3 MeV alphas are mainly generated within the sphere, while those produced outside drop below the cutoff energy and do not reach the sphere either.

In fact, I obtained the analogue graphs to the ones you showed for FLUKA’s current, but calculated with PENHAN, and they are similar (see electron_spc.png).

Regarding your last point “when you rose the production cutoff to 10 keV in FLUKA: you effectively forced deposited in the sphere the energy carried away by delta rays …”, I understand that I should observe the same effect by maintaining the production cutoff at 1 keV but increasing the electron transport cutoff (via the EMF-CUT transport card) to 10 keV. However, with this setup, I still obtain the lower dose value.

Here I include more details on my observations that may be useful to understanding the problem I am facing:

• To isolate the source of discrepancies, I repeated the PENHAN simulations but used the stopping power values generated by FLUKA. The results (table_2.png) show that percentage variations are now very low - below 0.5% in most cases - except for 3 MeV. This confirms my assumption that the primary source of discrepancy was the stopping powers used, and that something unusual is happening in the 3 MeV alpha case.

• When analyzing the alpha fluence inside the sphere for 3 MeV calculated with FLUKA with the delta-ray production cutoff set to 10 keV (input file alpha_2.inp in the first entry), the artifact near 3 MeV disappears (fluence_3_mev_deltaray_10_kev.png). This suggests that:
  – The fluence artifact is related to the lower dose for 3 MeV, since its absence results in a less pronounced dose discrepancy with PENHAN.
  – Something unusual is occurring in FLUKA’s delta-ray production process for this energy.

• I performed additional FLUKA simulations with both transport and production cutoffs set to 1 keV (input file alpha_1.inp in the first entry) for energies around 3 MeV. The results of the alpha fluence within the sphere (low_energy_fluences.png) show that the artifact consistently appears in the same position, around 2.8 MeV. This suggests that something is happening around this specific energy, though I cannot yet determine what it is.

• Finally, I repeated some of the simulations using other materials instead of water, to test if the artifact was specific to alphas in water, but I still observed it (fluences_other_mat.png).

I hope these details provide more insight into the issue.

Thank you again for your assistance.

Best regards,

Lidia

[cesc (Francesc Salvat Pujol)]

Dear Lidia,

Apologies for the delay.

We can thus far report that the depletion in the alpha fluence you see right below 3 MeV is due to the runtime fluctuation of the effective charge, which indeed impacts delta ray production.

We’ll look further into it, investigation will carry on.

With kind regards,

Cesc

[cesc (Francesc Salvat Pujol)]

Dear Lidia,

We’ve meanwhile looked at the issue in more detail.

The culprit was indeed the runtime fluctuation of the effective charge. We have a tentative patch in the making, which will make the alpha fluence go from what you reported, i.e.

to the following tentative picture:

…bringing also the dose from the 106 mGy in the 7 um-sphere to 110 mGy.

A few additional checks are now in the pipeline. If everything passes this will be released in one of the upcoming versions of the code, ideally still this year. NB: the effective charge itself will be unaltered, simply its runtime fluctuation will be somewhat smoothed out.

Thanks once again for pointing out this issue.

With kind regards,

Cesc

[lpalenciano (Lidia Palenciano Castro)]

Dear Cesc,

Thank you very much for your response. I’m glad to hear that the issue is being addressed, and I look forward to seeing the improvements in the upcoming releases. Thank you for your efforts.

Best regards,

Lidia