DOSE normalisation if not all particles are in considered area

[TashaSpohr]

Dear FLUKA people,

I have a question regarding the normalisation of the dose if the considered volume is smaller than the beam.
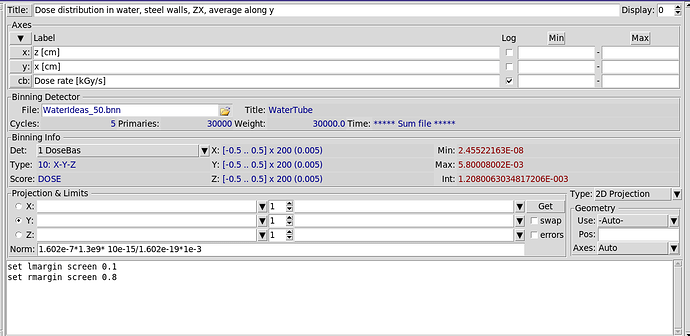
As I understand it, the dose (from USRBIN) is given in GeV/g per primary particle. For normalisation in a plot I must multiply by 1.602e-7 to have it in Gy.
Then, with my electron beam with a repetion rate of 1.3GHz, 10fC for example, I would also multiply by 1.3e9 * 10e-15/1.602e-19 to get Gy/s for all electrons.
I am pretty confindent that I understood that correctly. However, this normalisation only makes sense when I plot the entire volume, right?

For example: I have a test experiment here with a steel tube and water inside. The electron beam irradiates it and I want to know the dose rate at every point. But I only know how to normalize, if I average over all y (when plotted in XZ plane, like in the attached figure).

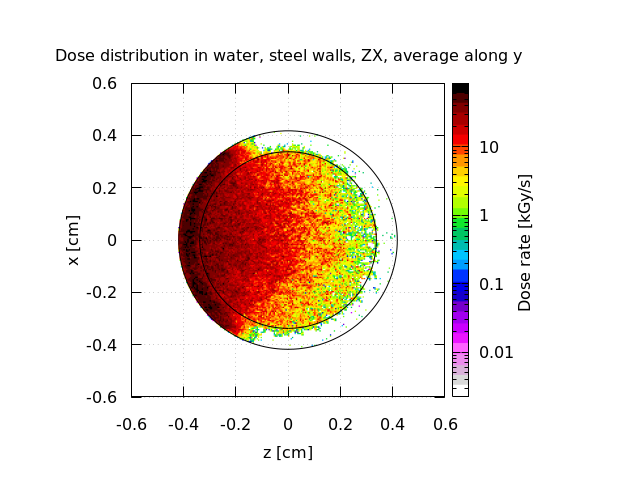
If I only want to look at the dose rate around y = 0, there would be much less electrons in that area. So I wouldn’t have 10fC there, but just a certain fraction. How do I account for that? I dont want to have to normalize per primary particle.

Do I need to get the amount of electrons in that area using some sort of tracking and then use that fraction to get the “real charge” in that area? Or is there a much simpler way?

I would appreciate some help!
Thank you and best regards,
Tasha

[ceruttif (Francesco Cerutti)]

Hallo @TashaSpohr
Provided that you input (in the BEAM card, or through a source routine) the real beam transverse distribution (in the xy plane, assuming that your beam is directed along z, which I’m not fully sure is the case you modelled), the simple normalization you elaborated is correct. In fact, FLUKA results are given per beam particle belonging to the input distribution, and so you need to multiply by the number of beam particles corresponding to the whole distribution, no matter if only a fraction of them impacts the region of interest (this is already taken into account in the FLUKA result, which makes the simulation helpful).

On the other hand, independently of the normalization (that is established once forever according to the above), the averaging over the third (missing) dimension (say y) - through the respective y-interval limits, or absence of limits, in Flair - is something to pay attention to. If your beam distribution is uniform along the considered y-interval, then you can safely average the dose results to profit from increased statistics. But if no uniformity is expected, then averaging will artificially lower the local peak dose value, which often is what one is interested in.