Energy loss distributions for heavy ion in silicon

Scoring
1

Dear FLUKA experts!

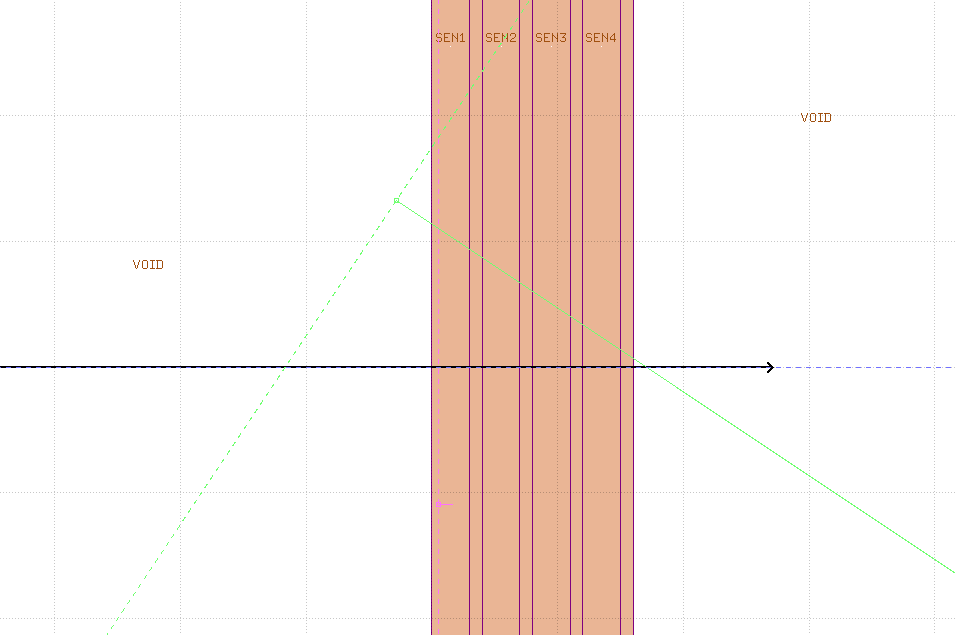
I have a basic setup with a few silicon layers in a row (see pic below). Some of them (SEN1-4, 300 um thick) are used for scoring energy loss via DETECT card (sensitive regions) and some are non sensitive with a 100 um thickness.

image
image955×635 4.77 KB

I am calculating various setups (1 layer of silicon, several layers of silicon etc) with initial particles as protons with 1 GeV energy and heavy ions, namely Fe with energy 1 GeV/n.

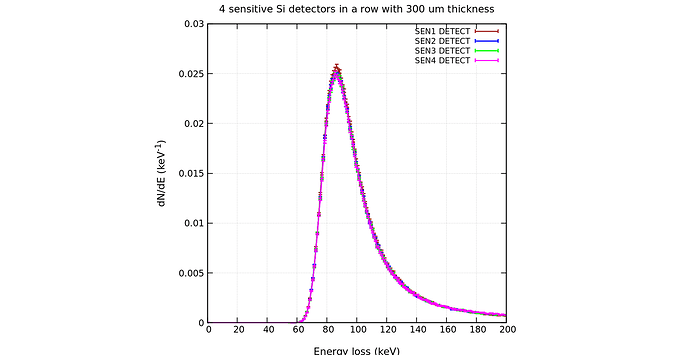
In the setup, where I have all the layers enabled, with a proton as initial beam particle, I am obtain such plot:

image
image1846×952 60.6 KB

Where all the distributions following the Landau distribution and almost lay on each over.

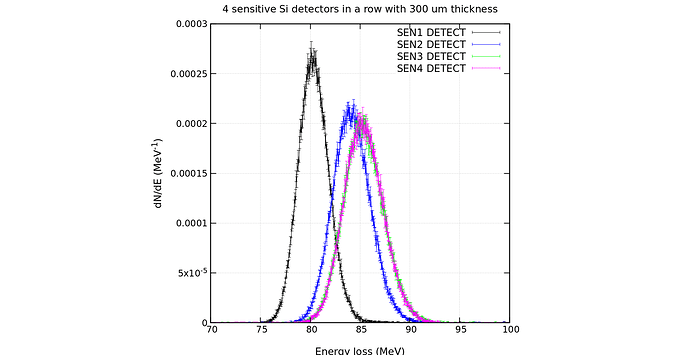
However, if I am changing the initial particle to the Fe ions (A=56) with the energy of 1 GeV/n. I see these plots:

image
image1846×952 85.3 KB

The bell shape is understandable, but why the 2nd, 3rd and the 4th distributions are shifted? Also, the 3rd and the 4th are almost lay on each over and others are not… Indeed, the expected distributions should be a bit shifted to the higher energy, but not that much, the distance between the means of the first and the second distributions is about 4 MeV. I did a simple calculations using WebAtima and I am getting average energy loss at around 88 MeV in the first silicon detector (SEN1), but FLUKA gives about 80 MeV (mean of the normal) for the SEN1 which is 8 MeV different! For the over detectors: SEN2-4 I am getting almost 88 MeV via WebAtima as well, but with FLUKA, SEN2 has about 84 MeV and SEN3/SEN4 have about 85 MeV which is still far from ATIMA results.

Also, if I am decreasing thickness of the sensitive detectors to the value of 100 um, I am getting this picture:

image
image1846×952 80 KB

Which is almost the same situation to the previous one, WebATIMA says that SEN1-4 will have average loss about 29.4, but FLUKA gives 26 MeV for the SEN1, 27.4 MeV for the SEN2 and about 28 for the SEN3 and SEN4, which is closer, but still different.

Am I doing something wrong, or missing? I’ve checked the input and it is seems fine, but maybe I am wrong. I thought that distributions for the Fe ions will be normal with the means at about the same values from ATIMA, they should lay very close to each other and just a little bit shifted.

Please see the input, flair, *lis and results from the WebAtima attached below.
Best regards,
Ivan

EnLoss.flair (16.1 KB)
EnLoss.inp (4.8 KB)
webatima_result_56Fe_100um.txt (2.7 KB)
webatima_result_56Fe_300um.txt (2.7 KB)
SEN1-4_Fe_17_tab.lis (180.3 KB)
SEN1-4_Fe_100um_17_tab.lis (180.3 KB)
SEN1-4_prot_17_tab.lis (180.3 KB)
SEN1_100um_17_tab.lis (180.3 KB)

2

Dear Ivan,

Your DELTARAY card is ineffective: you request a delta-ray production
threshold of 1 keV but do not specify the material, whereupon the
default WHAT(4)=HYDROGEN, WHAT(5)=WHAT(4), WHAT(6)=1 are taken. You are
left with a delta-ray production threshold of 100 keV as per DEFAULTS
PRECISIOn.

This means that collisions of your p/56Fe on a target e- leading to
energy transfers larger than 100 keV to the e- are explicitly sampled
and the resulting delta ray is tracked, possibly carrying its energy
away (!).

Consider instead the somewhat simpler picture one has in mind when
taking the (unrestricted!) stopping power to estimate energy deposition.
This implicitly assumes that all energy transfers to target e- are
locally deposited. This turns out to be an overestimation:

  • The range of 100 keV e- in Si is around 100 um
  • The range of 3 MeV e- (that should be the maximum energy transfer they
    can pick up at the energy you’re working at, arithmetic errors
    aside…) in Si is even longer

So energetic delta rays can travel to neighboring Si slabs in your
stacked geometry, depositing their energy elsewhere (!). This helps
explain the shift to smaller energy losses in the first slab. The
subsequent slabs still suffer somewhat from the same effect, but a bit
less, as they are probably fed from upstream delta rays.

One last ingredient: the differential cross section for delta-ray
production scales like the square of the projectile charge. So delta-ray
production by 56Fe ions is a factor 26^2=676 more effective than for
proton. This could help explain why for p you’re fine, whereas for 56Fe
the effect is accentuated.

Finally, if you really want to reproduce the (unrestricted-)dE/dx
overestimate, e.g. to make sure that the deposited energy falls within
your dE/dx estimate within very few %, simply raise the DELTARAY to some
high value (3.5 MeV should suffice).

Hope this helps,

Cheers,
David

4

Dear @horvathd !

Oops… Seems I just missed this part… Huge thanks to you, Dávid! Your following considerations are exactly what I thought and I was wondering why when I changed DELTARAY value everything was staying as it was… I need to be more careful. Thanks a lot for clarification!

Regards,
Ivan