Dear Fluka Users,
I am trying to determine the radius of a charged particle’s trajectory in a magnetic field. As a starting point, I chose a proton beam with an energy spectrum of 1 MeV to 100 MeV and a magnetic field strength from 1 T to 3 T.
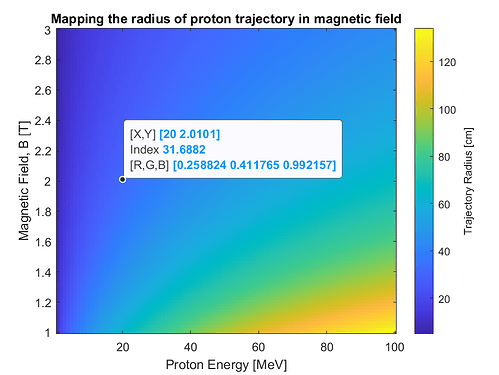
First, I created a map to plot this relationship between the proton energy, magnetic field strength and the trajectory radius on MATLAB and attached the map here.
Now, I am trying to validate my results with FLUKA and would like to get the radius values for several proton energies and magnetic fields.
I did some visual inspection after plotting the beam trajectory by using a USRBIN card for a chosen scenario, for example, 20 MeV proton entering in magnetic field of 2 T. The radius from MATLAB calculations I found is approximately 31 cm whereas, in FLUKA plotting, I see it is around 34 cm.
If we ignore my near-hit calculations, is there any way to get radius values for an energy and magnetic field spectrum? It is similar to finding mass attenuation coefficient, I assume, but for a 2-dimensional matrix scenario, i.e., proton energy and magnetic field. So it might be a little bit more tricky than finding MAC.
I am sort of a beginner and finding user routines challenging. So it would be great if there were any FLUKA user routines to carry even a similar work. Please let me know, many thanks!
Kindest regards,
Gokhan