Hexagonal lattice with large number of elements

Geometry and Materials
1

Hello,

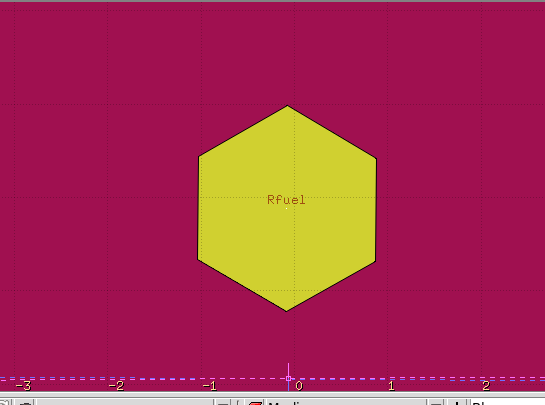
I’m trying to create a hexagonal lattice with 3 different ‘prototypes’, similar to the one below.

screenshot22

The prototypes are not single regions and so my understanding from reading other posts is that the best option is to use the LATTICE card with the ROT-DEF. My understanding is that I define a single LATTICE card which details the lattice container and then I have a ROT-DEF card which defines the coordinates of each lattice element. I have a lot of lattice elements which would result in a large input file but there doesn’t seem to be an easier way of doing this.

In order to simplify the problem, it would be easier to define the lattice spacings as parameters using #define and then input the coordinates as such:

#define    w
#define    s

Lattice element            X         Y         Z
          1                $w        $s        0
          2               2*$w      2*$s       0
          3               3*$w      3*$s       0
etc.

but it seems like it’s not possible to define mathematical expressions in the geometry cards? According to this page FLUKA: 6.1} The input preprocessor it’s possible to use mathematical expressions in the #define card but this doesn’t seem to be working in my input.

I have attached my input. So far, I have created the lattice prototype but have not yet implemented the lattice.

snre_gcr_spherical_source_v3.flair (12.6 KB)

Thanks,

Emma

3

Dear Emma,

Can you please clarify visually which part you want to replicate?
If it’s only this piece,
image
you will not benefit from the lattice feature.

Geometry definition and #define supports mathematical expressions:
image
But to place every rod in the active zone you will require some loop with proper logic inside,
which is unfortunately not possible in Flair.

I suggest you select and construct a symmetric sector of the active core
and then replicate it with rotation (alternatives also exist). It will speed up your simulation by reducing the number of geometry zones inside the region by symmetry factor.
Be aware that two lattices cannot touch, so you need a buffer region between them.

EDIT: With the right geometry configuration touching lattices shouldn’t cause problems

image
image1550×413 37.4 KB

I attached a very simple example of this.
simplified.flair (3.0 KB)
simplified.inp (2.8 KB)

Cheers,
Volodymyr