Dear Francesco
Thank you very much for your reply. As suggested by you, I’ve checked the TCQUENCH card. According to the Fluka manual, the TCQUENCH card provides calibration constants, time cutoff parameters or Birk’s law parameters. I guess you are referring to Birk’s law coefficents. I was checking this topic in some textbooks and I’m actually not sure, if Birk’s law is equivalent to my problem. To clarify, I repeat here my goal/problem in more details:
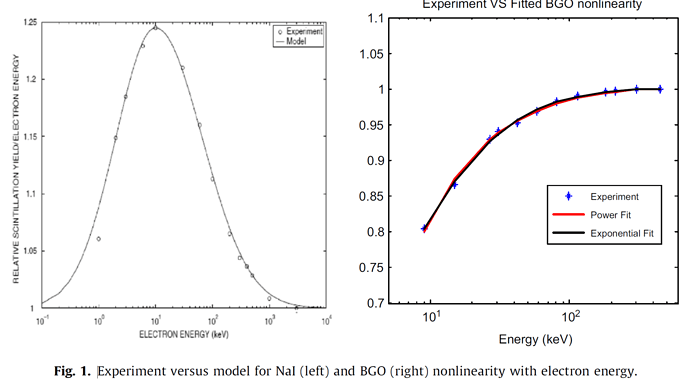
According to some publications already cited in the previous post, there is a non-linear scintillation efficiency present for electrons in inorganic scintillators (Nai(Tl), BGO,…), i.e. the number of scintillation photons is not proportional/linear to the deposited energy of the electrons. Therefore, to correct for that issue, one has to multiply each deposited energy by electrons (events, where electron energy goes below the energy threshold (local) as well as continuous energy loss) by the corresponding scintillation efficiency:
E_detector(E_e_deposited) = ScintillationEfficiency(E_e_deposited) * E_e_deposited
For the ScintillationEfficiency(E_e_deposited), there exist empirical functions (cf. [4] from above). I’m also attaching a figure from this paper, which shows the general shape of the ScintillationEfficiency(E_e_deposited). To obtain the total energy deposited per history/primary (E_event), one has to sum all electron interactions in the detector crystal volume plus some other energy deposition events by photons:
E_event= sum (E_detector) + …
This E_event is provided by the detect (+usreou.f routine) or eventbin card, but of course without considering the effect described above, i.e. ScintillationEfficiency(E_e_deposited) =1.
So, I have the following questions for you:
- Is the TCQUENCH card able to account for the described effect? I’m not entirely sure, if Birk’s law is the same as the effect described above. Birk’s law seems to be related to quenching, which seems to be only relevant for ions at high energies. In addition, Birk’s law seems to cover only continuous energy loss and no local energy deposition events by electrons. Or am I wrong on this? To be honest, I do not see a way to enter an energy dependent scintillation efficiency in the TCQUENCH card.
- Is there maybe another way than the TCQUENCH card. In the meantime, I’ve found this discussion on the forum: Charge trapping using comscw.f routine. It’s covering a similar topic, but unfortunately, no final solution was provided.
Thank you very much for your support. I really appreciate that!
Cheers,
David