Dear Artemis,
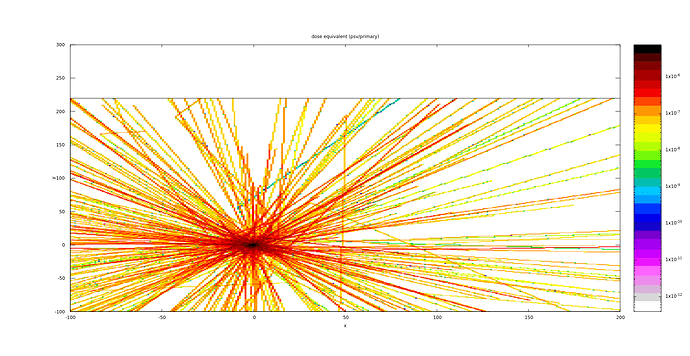
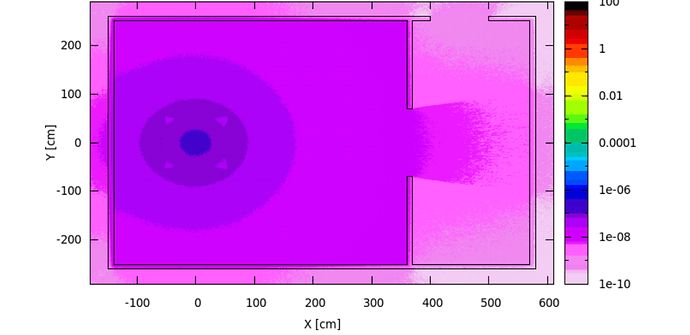
The fact that in your neutron dose equivalent plot you clearly see contributions (tracks) of individual neutrons indicates that the number of histories you are running is not sufficient. In most areas of your geometry, except close to the target, hardly any neutrons arrive and therefore the plot is not populated.
Why is this not the case for the photon dose equivalent when you run the same number of primaries? Simply because a significantly higher number of photons are produced in each history, compared to neutrons.
What to do? Taking a direct approach, you need to increase the number of histories. You will have to determine by how much, it looks as if a factor of 100 would be the minimum.
An alternative/complementary approach is to apply some biasing to the relevant physical process. The neutrons in your problem are mostly not generated directly by the impacting electrons, but by the secondary (bremsstrahlung) photons, which induce photonuclear reactions in the target, e.g.:
γ + ^{208}Pb \longrightarrow ^{207}Pb + n
(γ,xn) reactions have low cross-sections and many photons will go through the target without interacting. You can artificially increase the probability by reducing the interaction length of photons in the target. This is not cheating: the code then adjusts (reduces) the statistical weight of the generated neutrons in order to still get the physically correct result.
You can apply this biasing via the LAM-BIAS card.
Take a look at the biasing lecture from the FLUKA course (look for mean free path biasing, but also look at the introduction):
As a further note, keep in mind that the threshold for (γ,n) reactions in lead is above 7 MeV (photon energy), and the bremsstrahlung spectrum decreases exponentially up to the electron energy, which here is only 12 MeV. So only a small fraction of the generated photons have sufficient energy to induce neutron-producing reactions. This is to reinforce the point of why few neutrons are produced, and why biasing may be a good way to go.