Dear Giusepe,
I found a bug implementing the subroutine sample_annular_distribution_sin2theta. This code solves the cosz divergences by comparing the original sample_annular_distribution available in the new_source_gen.f
subroutine sample_annular_distribution_sin2theta( rmin, rmax, axis_1, axis_2)
use source_library implicit none double precision rmin, rmax, axis_1, axis_2 double precision sin_theta, cos_theta, sin2_theta_min, sin2_theta_max, sin2_theta double precision radius, rmin_squared, rmax_squared double precision FLRNDM, xdummy double precision h h = 7200000.0D0 call SFECFE( sin_theta, cos_theta ) rmin_squared = rmin * rmin rmax_squared = rmax * rmax sin2_theta_min = rmin * rmin / (h * h + rmin_squared) sin2_theta_max = rmax * rmax / (h * h + rmax_squared) sin2_theta = sin2_theta_min + (sin2_theta_max - sin2_theta_min) * FLRNDM ( xdummy ) radius = h * sqrt(sin2_theta / (1.0 - sin2_theta)) axis_1 = axis_1 + radius * cos_theta axis_2 = axis_2 + radius * sin_theta return end
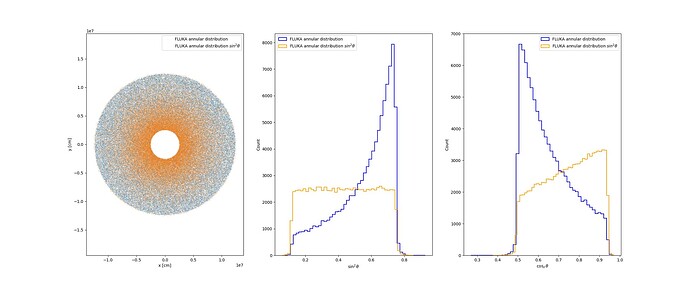
The plots below show the annular distributions, the distribution in sin^2 \theta and cos_z \theta. Now the divergence in cosz has disappeared and the distribution in sin^2 \theta is flat.
The cosz are obtained for the first inelastic interaction using the entry USRDRAW and not from its first appearance as you suggested using SODRAW because I could not write the information correctly. If you can help me with the SODRAW entry I can compare both distributions and close this discussion.
Many thanks and have a happy new year!
Jordi