Dear experts,
In the previous question, I changed WHAT(2) in USRBIN to DOSE-EQ, and the result I got is shown in the figure. I am still confused about how to convert the dose equivalent in the result into the dose equivalent rate, and how to realize the calculation by beam intensity mentioned earlier.
And What is the meaning of the unit “pSv” of DOSE-EQ?
pSv means pico-sievert, i.e. 1E-12 Sv.
(Prompt) DOSE-EQ results are given in pSv per primary beam particle. To get a dose equivalent rate, you need to multiply by the beam current (i.e. beam intensity rate, such as number of bombarding protons per second, yielding eventually pSv/s), using to this purpose the Norm field in the Flair plot frame you reported above. Note that the values in the figure are averaged over your whole 12 m scoring z-interval, which normally makes no sense. The Flair plot frame allows you to limit the third dimension interval over which the average is performed to a more meaningful range.
Thank you very much for your answer.
And here are some of my questions.
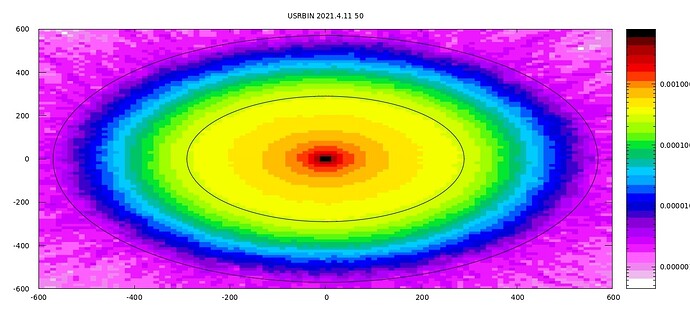
1.As shown in the figure, I set the range on each axis. Does this setting mean the dose equivalent in the z=0 plane?
2.In the dose equivalent diagram, the dose equivalent at point (600,600) is 0. Is it because the number of neutrons is too small?

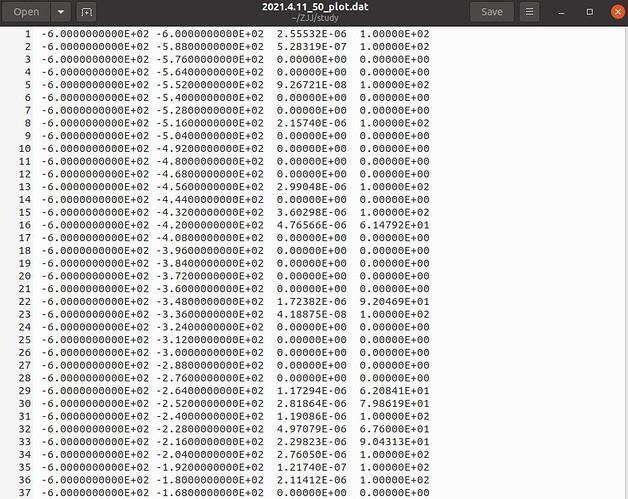
3.In this table obtained by running the software, will the data change with the change of range setting? Or, what is the meaning of this data? Is it an average value?
4.How to get the beam intensity? Is it obtained in software or in background information? What is the unit of beam intensity and its meaning?
Dear @Junjie_Zhang,
Can you please share the entire flair window for your first question?
Thanks
- With those plot settings, you are plotting a dose equivalent map in the xy plane, with values averaged over the (-20,0) z-interval.
- You obtain zero because in the simulation you get no neutrons there, due to insufficient statistics. So you have no estimation of the actual value there. In order to achieve it, you should increase your statistics accordingly.
- Obviously the third column (fourth in your screenshot), containing the dose equivalent values, will change depending on the considered third dimension (z) interval, over which the dose equivalent is averaged. Note also the last column, with the statistical error in percentage.
- The beam intensity is a piece of info that one needs to know independently of FLUKA, to be used to normalize the FLUKA results. I already answered about its units and meaning: if you have a proton beam, it’s the number of beam protons. For a rate calculation, you need to know the beam intensity rate, i.e. the beam current: number of protons per second. If you have the beam current in mA, you should be able to transform it in p/s.
Thank you very much for your answer.
For the first question, I want to know how to set the dose equivalent rate in a certain plane instead of the average value in a certain interval?
For the fourth question, I made the following calculation:
I multiplied the result of USRBIN by the beam intensity (A) divided by 1.6E-19 multiplied by 3600.
Is my calculation correct? Is the result obtained in pSv/h?
There is also an extended question, will the setting of neutron number affect the result of dose equivalent rate?
I’m sorry to bother you again, and look forward to your reply.
You cannot get a spatial distribution on a plane, but you can adapt the third dimension (z) resolution such as to average on a reasonably small interval. According to your present grid, with 20 cm z-bins, the minimun average interval is 20 cm, but you can change the grid and thereby get an average over few cm only, which for neutrons is a suitable approximation of a plane.
Yes.
What do you mean with setting of neutron number? Number of simulated histories as requested in the START card? (Isn’t yours a proton beam?) Of course the statistics affects the dose equivalent result! It’s the Monte Carlo foundation, to get a reliable result you need to achieve a suitable statistics, whose quality is reflected by the respective statistical error.
Thank you for your reply. It was my mistake to write protons as neutrons.
I’m a little confused that the result obtained by USRBIN is the influence of a single particle, and the dose equivalent rate should be affected by the number of particles emitted per unit time (beam intensity). Why does the setting of the number of particles affect the dose equivalent rate?
Maybe I misunderstood the unit of USRBIN results in the manual. Doesn’t it represent the influence of a single particle?
The FLUKA results, and specifically the USRBIN ones, are always normalized to one beam particle. The beam intensity is a factor to be used to scale them to your real case. But if you ask FLUKA to simulate one proton, thousand protons or million protons, the FLUKA result will not be the same. Imagine that you are interested in the neutron dose equivalent in a particular location, as you are. In the first case you will get zero, because no neutron managed to get there; in the second case you will get something, possibly quite different from nearby values, because your statistics is still insufficient; in the last case you will get a reliable estimate, as the respective small statistical error will indicate. It’s the latter that tells you if the number of simulated beam particles is enough for your purposes (in your case, you will not need necessarily million beam particles, look at the statistical error at the location of interest and at the smoothness of the plot to judge if your statistics is fine or not).
Dear expert,
After reading your reply, I probably understood the significance of setting the number of particles. I also found that when I first simulated, the statistical error of many points was 100%. When I increased the number of particles ten times, the maximum statistical error became about 10%.
And I want to know, is there a limit for statistical error? (The calculation is meaningful when statistical error is less than this limit.)
Very good, that’s encouraging.
I’d say that 10% is a good limit for a point-like quantity (not necessarily for an integral quantity as the energy deposited over a region, where one would aim to a statistical error of few %). Take a look at this lecture, in particular slides 28-29.
Thank you again for your answer, I will study this lecture carefully.
Dear expert,
I have the same question as his first question, but I use grid in USRBIN.
I multiplied the result of USRBIN by the beam intensity (A) divided by 1.6E-19 multiplied by 3600.
Is my calculation correct? Is the result obtained in pSv/h?
And,I want to know how many particles per second the beam intensity 1A is?
Dear Junjie,
Yes, your normalization is correct if you scored DOSE-EQ over a mesh with USRBIN.
Dimensionally, a current divided by a charge is the inverse of a time so the beam intensity divided by the elementary charge gives you the number of particles per second in the beam: the “beam intensity (A) divided by 1.6E-19” is precisely that.
Cheers,
Davide