Dear expert,
The attachment is my file.
scintfiber.flair (3.0 KB)
This is a scintillation fiber. I used 10Mev neutron incident to record the energy deposition in the fiber and the optical photon flux at the material interface, but the result does not seem to be correct. The 1D project shows that the energy deposited at each point is much greater than the energy of the incident neutron(about 0.02Gev) , The flux of photons is also much greater than the theoretical value(the calculated value is 6.521E+13),For the process of scattering and losing energy to produce photons, it is almost impossible.Could you help me?
Dear @xiongbp,
Did you take into account properly the normalization? I don’t see any in your plot called “scintifiber_25_plot”.
I’m quoting the manual for the USRBIN card, note 5:
- Energy deposition will be expressed in GeV per cm3 per unit primary
weight. Doses will be expressed in GeV/g per unit primary weight. To
obtain dose in Gy, multiply GeV/g by 1.602176462E-7
which means that in each spatial bin you get an energy density [GeV/cm3] that cannot be directly compared to the initial neutron energy [GeV] (which by the way in your input is 1 MeV and not 10 MeV), apart from the fact that nuclear reactions alter the energy balance (consuming or freeing energy through energy-mass conversion). Still the main point here is that GeV and GeV/cm3 are not comparable as such.
As for the differential fluence from USRBDX, you get spectra in cm-2 GeV-1 sr-1 (double differential) and in cm-2 GeV-1 (angle integrated), whose integral is given in the sum.lis file.
When comparing numbers, always associate them to the respective units.
Dear @ceruttif ,
Maybe my questions are a little messy. I rearranged them and revised some questions. Please refer to the attached documents.
Firstly, the PROD card is based on the following principle: a neutron generates secondary particles through Li (n, a)T reaction, ionizes and deposits 4.786Mev energy in ZnS (Ag) scintillator, and the number of photons generated is 1.6e+05. It is assumed that the wavelength of all photons is 450nm,
Then fraction = (1.6e + 5) * 2.756/4.786=0.0921, where E is the energy of photons, E(ev)=1240/450= 2.756, is there no problem with this calculation?
My questions are as follows:
- In USRBDX, the output is set to < x > * y, X Norm is set to 1/ev, and X and Y do not set log. Why does the number of photons displayed on the output Y axis exceed 1.6e + 5, about 4e+05?
- In order to simulate the detection efficiency, I want to get the calculation results under multiple incident neutrons instead of per primary. How should I set it?
Look forward to your help.
mix.flair (2.5 KB)
Dear Xiong,
Unless I overlook something, there is a mess of units: the 4.786 are in MeV, whereas the 2.756 should be eV, so there appears to be a factor 1000 dancing (which probably cancels out with a missing number of primaries, 1000 in your case, and you get the a consistent result in an accidental way).
One check you can do is to write down the following quantities (pick values up from the *001.out fie):
- Energy deposited per primary (
Edep) - Fraction of deposited energy that goes into optical fotons (
fr) - Total (unweighted!) number of optical photons generated (
Noph). Note that this is indeed an absolute number, not divided per primary. - Number of primaries (
Nprim). - The optical photon energy (
Egamma), which in your case is unique.
You could then check that Noph = Edep * Nprim * fr / Egamma
NB: this quick check works because you have a single optical photon frequency.
(The primary energy is not of terrible concern to answer the question, but do note that in the post above you claimed 10 MeV energy, which turned out to be 1 MeV, and now we have ~thermal energies instead… just make sure you run with you intend to run.)
The point of displaying quantities as <x> * y is to have a faithful representation of the considered spectrum in a (at least horizontal) log scale, as carefully elaborated upon in this post: Understanding USR-1D plot - #11 by xiongbp
Selecting <x> you de facto request a proper treatment of the Jacobian for going from linear to log horizontal scale. If you plot <x>*y in a linear horizontal scale, this defeats the purpose. I now fail to see how one could extract quantitative info from such a representation.
Also, note that your USRBDX looks at whatever optical photons go from region MIXTURE (which is just the very first segment of your target!) to region BLANK. You may want to revise this.
You’d simply need to scale your Monte Carlo results (given per primary) by the intensity of the neutron beam (all you need to know is how many neutrons impinge on your sample to scale the results accordingly).
With kind regards,
Cesc
Dear@ceruttif
I have a mistake about “fraction = (1.6e + 5) * 2.756/4.786=0.0921”,it should be “fraction = (1.6e + 5) * 2.756/4.786e+6=0.0921”,but the calculation result is correct.
Question:
2.I originally wanted to know the overall result obtained when N particles are incident, not the result of a single particle multiply N, but this seems to be unachievable, so we maybe not need to discuss it.
1.I am sorry for the energy mess,just take thermal energy as an example,as the attached file show.In my file,I scored three named count,energy and photon.
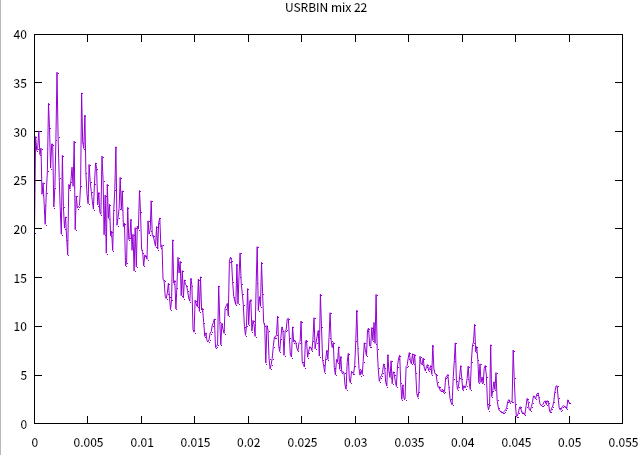
(1)“count” is photons’ number(set < x >*y) at the interface of “MIXTURE” and “BLANK” (length=0.05),the 1D projection of “photon” at length=0.05 should be equal to “count”,but it seems not,why?
(2)The 1D projection of “energy”,Y-axis is Gev/cm^-2,but the simulation value seems too large and not correct.

mix.flair (3.2 KB)
Dear@ceruttif ,
For above first question, the flux value of USRBIN with 1D projection at a specific length(dz) should be equal to USRBDX at the same length(dz),but it seems largely different.
At tab.lis, count of “integrated over solid angle” is much lower than the sum of “number of solid angle intervals”,how it to be?
The second question, the area is about 0.00785cm^-2,y-value is about 30Gev/cm^-2 at a specific length(dz),their result is about 0.2355Gev(dz),this value is too large to reliable.
The result corresponding to N incident neutrons is exactly the product of the FLUKA result given for one incident neutron times N, therefore it’s all but unachievable (even at plotting level inside Flair, where one can easily renormalize by N).
You scoring area is 0.00785 cm^2, over which you get an average energy density roughly decreasing from 30 to 20 GeV/cm^3 for z up to 0.01 cm (take 25 GeV/cm^3 as the average from z=0 to z=0.01 cm). This means that about 2 MeV are deposited from z=0 to z=0.01 cm, which is not too large. From your USRBIN-22 plot, one concludes that 3 more MeV are then deposited from z=0.01 cm to z=0.05 cm. Nothing is strange there.
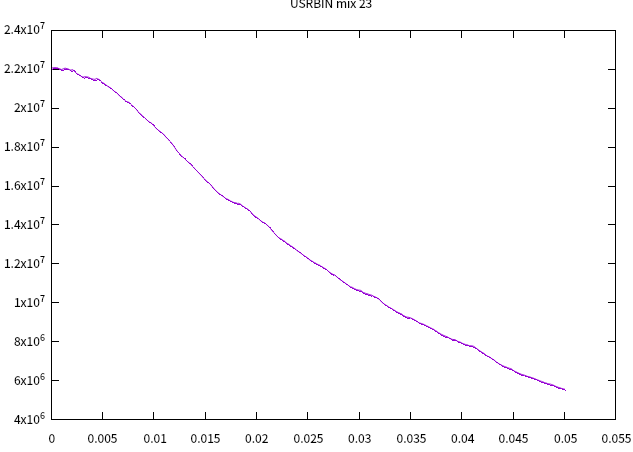
Your USRBIN-23 gives an optical photon fluence of about 6 10^6 cm^-2 at z=0.05 cm. Your USRBDX-21 gives an integral of 1.7 10^4 (look at the sum.lis file content), to be divided by the above area in order to get a fluence value, turning out to be 2 10^6 cm^-2. The difference (only one third of the expected value is found) is due to the fact that you limited the USRBDX scoring to one-way fluence and 2 sr. If you extend it, as it should be done for a meaningful comparison, to two-way fluence and 4*pi=12.57 sr, you would get an integral of 4.7 10^4 resulting into a fluence of 6 10^6 cm^-2 that matches well the USRBIN number.
Note that your spectrum graph is not suitable for calculating the integral (that is already printed for your convenience in the aforementioned sum.lis file): the value you read in your graph (~3.2 10^5) should be divided by the respective energy (almost 3 eV) and multiplied by the respective energy bin width (~0.15 eV), this way landing on the reported 1.7 10^4.
You are comparing once more different units/quantities: each term of the sum should be first multiplied by the respective solid angle in sr if you want to get back the number “integrated over solid angle”.
As a general attitude, you may want to consider that it’s objectively highly unlikely that FLUKA suffers from so huge incongruities as the ones you report and, as you meet them, you may want to try to find yourself the flaw in your reasoning - which is much more rewarding - before rushing at posting your contradictory findings and waiting for an answer. Of course, if eventually one does not manage to figure out what is wrong, this forum remains a resort always available.
Dear@ceruttif ,
I am very sorry that I have brought you a lot of work because I did not think deeply about the problem. Thank you very much for your reminder and I will definitely pay attention to it in the future. In addition, your answer is very detailed, thank you again for your help.