Dear @andrei.hotnog ,
Thank you for your questions. I will try to answer the different points you raised, namely scoring the proton energy, LET and absorbed dose of the beam as a function of the depth. Besides, I take as reference the useful answer you have mentioned at the beginning (Strange LET shape for 800 keV protons in LiF - #5 by msabateg), since many points are relevant here as well:
-
Absorbed dose: You attempt to score the LET by performing the transversal integration of the deposited energy density (USRBIN). Actually, since the deposited energy density is the absorbed dose times the material density, that integral is close to the dose profile along the z axis. Following ICRP, we can extract a definition of the dose averaged over z planes, something like:
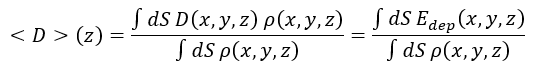
where D is absorbed dose, \rho is density and E_{dep} is deposited energy density. The numerator is actually what you plot in the graph, but unfortunately I don´t know how to obtain the denominator in FLUKA (it does not involve any radiation-related quantity). Nevertheless, this is simply the linear density of the volume under study and should be easy to obtain with some post-processing. Also, the values are normalised per primary particle. -
LET: Regarding the LET, in the reference we find different ways to score it. I will cover the deposited energy LET, the one you obtained, and the canonical tracklength-weighted LET. The normalisation is one of the main differences between them.
-
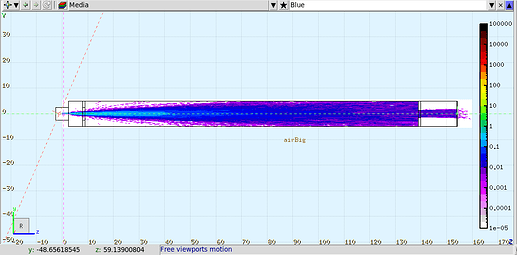
As you have correctly calculated, the deposited energy LET is obtained by transversal integration of the USRBIN result (plus surface normalisation and units). Your result seems fine to me, as long as the beam source normalisation is relevant to your case. Given the initial beam divergence, the long shape of your geometry and different layers upstream, many of the protons actually do not reach the volume under study. Thus, the per-primary-particle normalisation of USRBIN implies an underestimation of the scoring if you are interested only in the particles reaching the scored volume. The fluence USRBIN you have defined (see picture below) shows this qualitatively: the fluence reaching the detector is one order of magnitude (at least) lower than the initial fluence. That is the order of magnitude you miss.
You may want to obtain the fluence reaching the sensitive volume to correct the normalisation, which can be achieved with USRBDX:

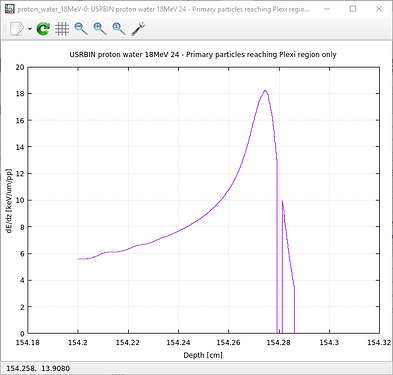
Then, changing the normalisation you reach values closer to the LET of a pencil beam in water (assuming that is what you mean by “expected values”):
Nevertheless, as explained in the reference, this definition is just an approximation with respect to the canonical tracklength-weighted LET and the correlation becomes worse for larger energies. There, the difference is almost 15% for 4 MeV protons, so let´s evaluate it for 18 MeV.
-
To obtain the numerator of the canonical LET formula you can use fluscw.f, together with USERWEIG, to weight the fluence with the function GETLET. I have implemented it as follows:
IF ((ISCRNG .EQ. 2) .AND. (JSCRNG .EQ. 6) .AND. (IJ .EQ. 1)) THEN
IF (MEDFLK(NREG,1) .NE. 2) THEN
IF (PLA .GE. ZERZER) THEN
FLUSCW = GETLET(IJ,SQRT(PLA**2+AM(IJ)**2)-AM(IJ),PLA,-1,MEDFLK(NREG,1)) * RHO(MEDFLK(NREG,1)) / 100
ELSE
FLUSCW = GETLET(IJ,-PLA,SQRT(PLA**2-2*PLA*AM(IJ)),-1,MEDFLK(NREG,1)) * RHO(MEDFLK(NREG,1)) / 100
END IF
ELSE
FLUSCW = ZERZER
END IF
END IF
I simply select the USRBIN of interest, protons as particles, leave aside the vacuum as material (problematic zero density) and correct the units (GETLET= keV/um/(g/cm3)). The denominator is retrieved simply with USRBIN scoring proton fluence (see the cards below):
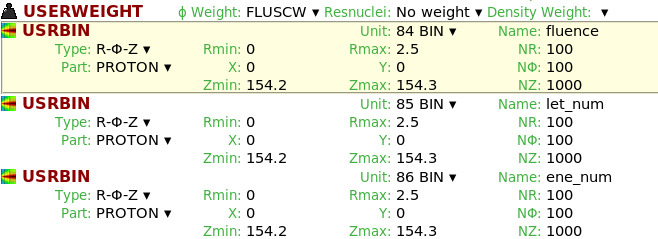
Finally, comparing both results below, we can see that the difference is quite important, since the deposited energy LET places the peak before the water, while the canonical LET peak is inside of the water. Canonical values are also x2 larger close to the peak. The interpretation of this difference is again the underestamation introduced by the constant normalisation of the deposited energy LET, compared to the z-dependent normalisation of the canonical LET.
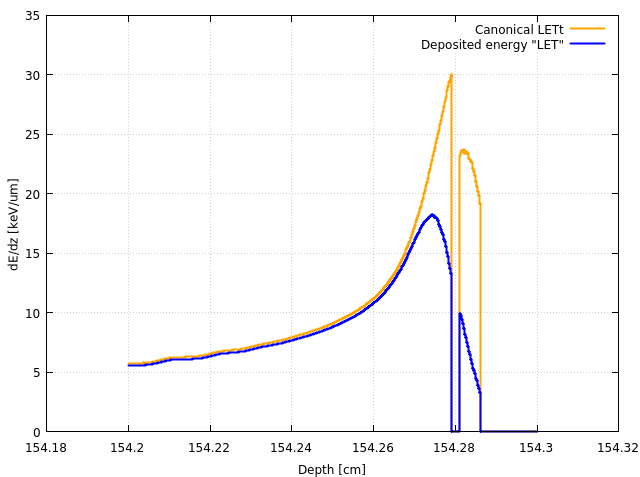
-
Energy: Concerning the proton beam energy along the axis, we can use a similar approach as for the LET, a tracklength-weighted energy average:
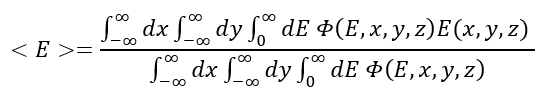
The denominator is the same one as for the LET, while the numerator is obtained via USRBIN as well with fluscw.f, but now using proton kinetic energy as weight:
IF ((ISCRNG .EQ. 2) .AND. (JSCRNG .EQ. 7) .AND. (IJ .EQ. 1)) THEN
IF (PLA .GE. ZERZER) THEN
FLUSCW = SQRT(PLA**2+AM(IJ)**2)-AM(IJ)
ELSE
FLUSCW = -PLA
END IF
END IF
This way we obtain the decaying average kinetic energy of the beam along the z axis. As observed for the LET, the beam is not fully stopped in the water and some protons exit with average energy 1 MeV:
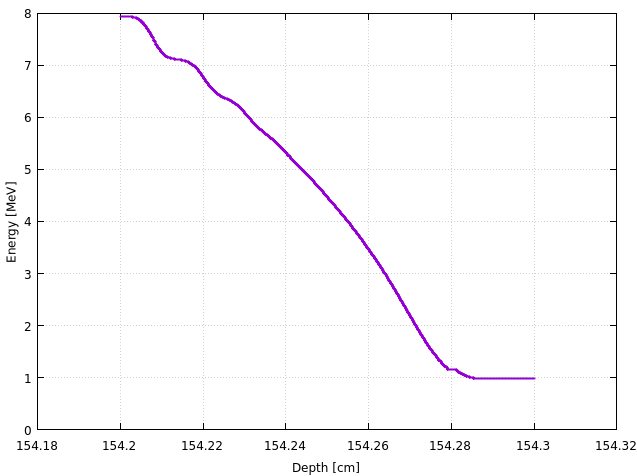
-
USRYIELD to score LET Lastly, about your question of scoring LET with USRYIELD, what you obtain is the fluence of particles crossing the surface as a function of the LET, and restricted for charges between 0.5 and 100.5 (for protons this only means you add a normalisation factor).

If you perform the LET-weigthed integral, you can retrieve again the average LET, which should be equivalent to the canonical LET (just a change of variables, plus the x/y integration already perfomed in the USRYIELD card).
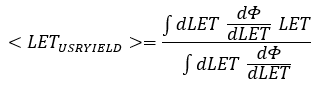
Nevertheless, please note that this is the value for a single z plane, you would have to score this over several planes to cover the whole length of interest.
This is all! Apologies for the lengthy answer, and let me know if you have any comments and whether this is helpful.
Mario Sacristan