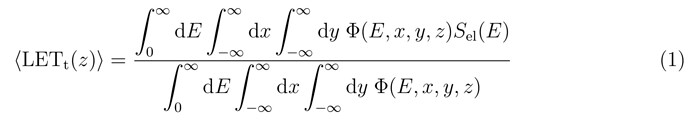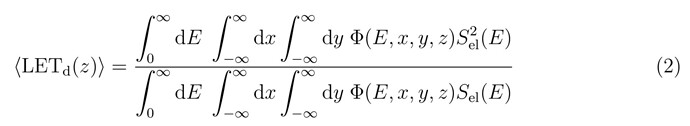Dear Enrico,
Just a minor comment in passing. We were curious how your method to score proton LET in depth (scoring ENERGY with a USRBIN and averaging over the transverse plane at various depths) compares against other definitions in the literature.
Definitions
“Canonical” definitions for the average LET at depth can be found e.g. in:
- https://aapm.onlinelibrary.wiley.com/doi/epdf/10.1118/1.4932217 (Eqs 1 and 2)
- https://nvlpubs.nist.gov/nistpubs/Legacy/IR/nistir5226.pdf (Eq 2)
The tracklength-weighted LET is defined as
where Φ(E,x,y,z) is the energy-dependent fluence at depth z (fluence integrated over x and y), and S_el(E) is the electronic stopping power as a function of E.
The dose-weighted LET is defined as
The fluence and the stopping power are to be evaluated/accumulated accordingly if one wishes to consider just primary particles, primaries and secondaries, a given charged particle species, etc. In the following it is assumed we evaluate the unrestricted LET for primary protons.
One can evaluate any of the numerators/denominators above in your problem by requesting to score e.g. BEAMPART or PROTON fluence in a Cartesian/cylindric USRBIN, invoking fluscw.f so as to weight the scored fluence with the requested power of the stopping power (calling GETLET as per Definition Function GETLET - #2). It’s then a matter of a bit of post-processing by hand to do the required ratios.
Instead, what the USRBIN scoring is doing when you request to score ENERGY (i.e. energy deposition density), take the 1D-projection and plot (multiplied by the surface!) as a function of z is (leaving aside contributions from sub-threshold particles) something a la:
Comparisons
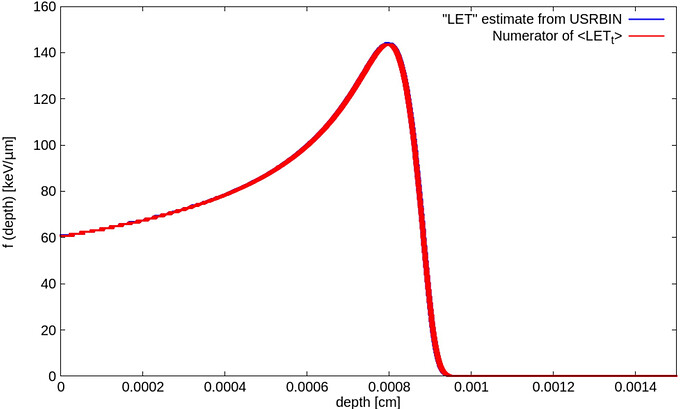
The last expression above (i.e. your USRBIN-mediated estimate of the LET at depth) essentially matches the numerator of <LET_t(z)>. The following figure displays (for your 800-keV p in LiF) in blue the LET estimate from USRBIN and in red the numerator of <LET_t(z)>. Note that they indeed overlap:
Fig 1. LET estimate with USRBIN vs numerator of <LET_t(z)>.
So far so good (at this low energy!). Here is the plot comparing your estimate vs the two definitions above, all overlapping reasonably well:
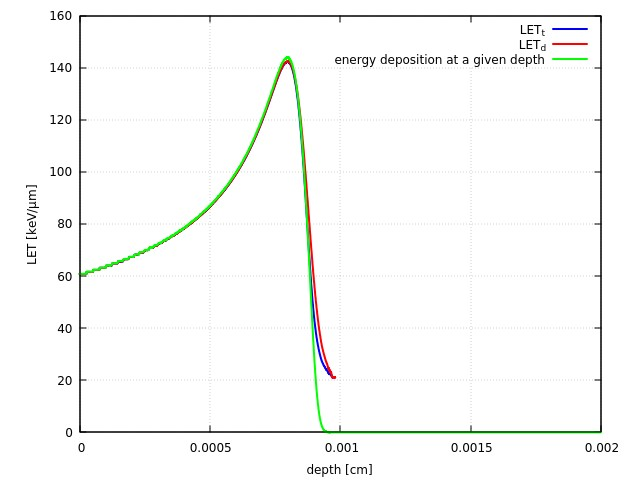
Fig. 2: LET estimates as a function of depth for 800-keV p in LiF
The scored quantity is still in relatively close relationship with the stopping power. Indeed, looking at NIST PSTAR one gets:
- ~60 keV/um for 800-keV proton → the three methods suggest 60 keV/um.
- ~140 keV/um maximum stopping power ever → the maximum in the curves above (corresponding to p at the end of their range) suggests ~140 keV/um.
However, as one raises the energy to say 4 MeV, the picture starts to change somewhat. Behold:
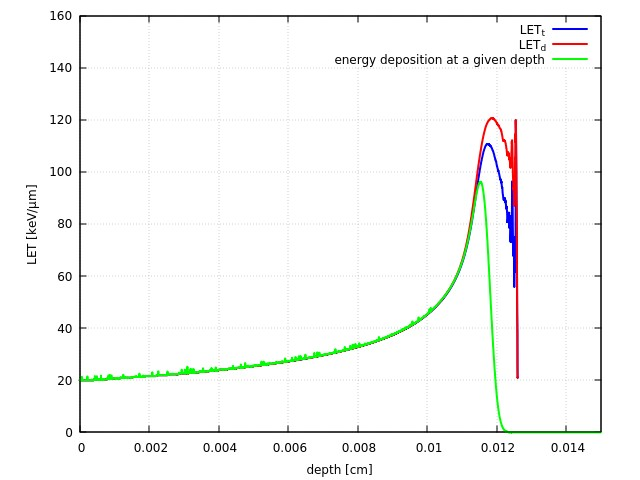
Fig. 3: LET estimates as a function of depth for 4-MeV p in LiF
A first comment: the two “canonical” definitions suffer from the fact that the fluence at the end of the range drops to zero, so one ends in a close to ~1/0 situation, which can be numerically problematic.
At the entrance of the LiF material, the p still have a reasonably well defined energy. The PSTAR dE/dx for 4-MeV p in LiF is indeed around 20 keV/um, in reasonable agreement still with the estimates. However, at depth (close to the onset of the Bragg peak), one observes two things:
- All three curves provide a maximum LET value ~15% lower than the actual maximum value of the dE/dx found above. It is therefore worth highlighting that one starts to lose a direct correspondence between the scored LET at depth and the actual stopping power, further elucidated below.
- The “energy-USRBIN” method drops even more than the other two definitions.
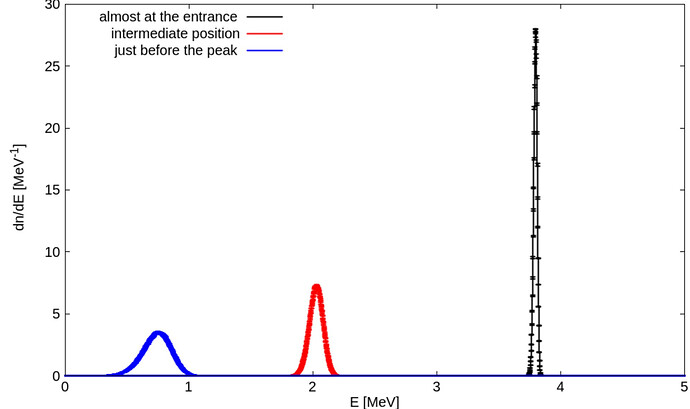
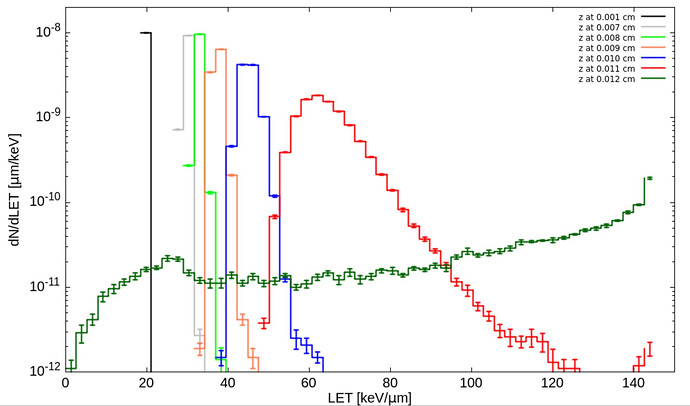
The overall drop from 140 keV/um to 120 keV/um near the Bragg peak is due to the fact that 4-MeV p have a longer range (0.013 cm) than 800-keV p (0.001 cm). This implies that energy straggling has a larger chance to act and to spread the proton energy distribution at deeper depths. In the following plot you can indeed see that the distribution of proton energies at various depths (at entrance, at intermediate depths, and near the Bragg peak maximum) progressively broadens:
Fig 4. Proton energy distribution at various depths in LiF for a primary energy of 4-MeV
This translates to an even more drastic effect in terms of the distribution of LET at various depths (scored here with a USRYIELD across fake planes at various depths):
Fig 5.: LET distribution at various depths in LiF for a primary proton energy of 4-MeV.
The broader the energy distribution at depth, the larger the range of LET that the protons probe. And considering the steep rise of the stopping power at lower energies, the more asymmetric the LET distribution at depth becomes. See e.g. the red curve. Thus, correlation with the stopping power at the energy expected at a given depth is somewhat lost (one gets an average LET value for an ever broader LET distribution at depth). This should explain the fact that all three estimates give lower LET values at the Bragg peak in Fig. 3 above.
Incidentally, your 800-keV case above is not affected by this, because the range of 800-keV is so short that energy straggling did not have a chance to act.
The fact that your “ENERGY-USRBIN” method drops even further than the tracklength- or dose-weighted LET definitions above is possibly related to the fact it does not take into account the division by the norm of the fluence as in Eqs. 1 and 2 above.
Summary
- Your proposed method to estimate LET at depth with USRBIN works (i.e. is compatible with the two formal definitions of <LET_t(z)> and <LET_d(z)>) only at energies low enough that energy straggling does not have a chance to sufficiently smear the proton energy at depth.
- At higher energies your proposed method deviates somewhat from the definitions found in the literature.
- The latter are numerically prone to numerical troubles at the end of the range as the fluence drops to zero (given the 1/0 behavior).
Best,
Marta and Cesc