Scoring both LETd and LETt of primary protons in water

Scoring
1

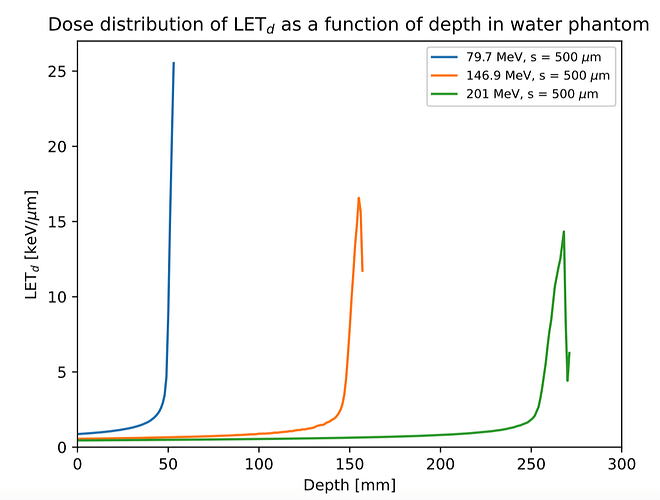
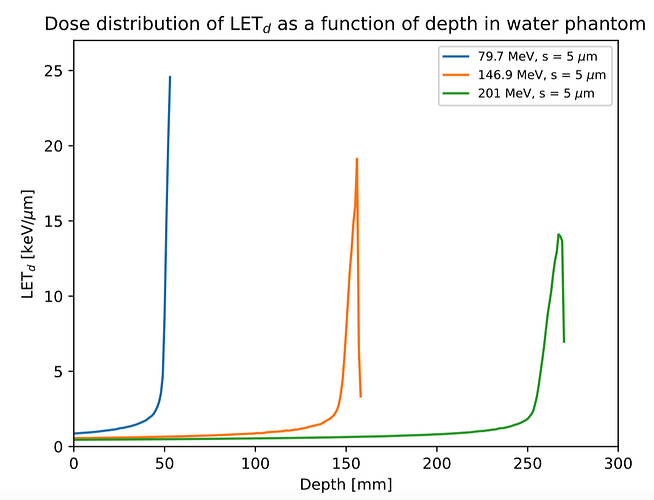
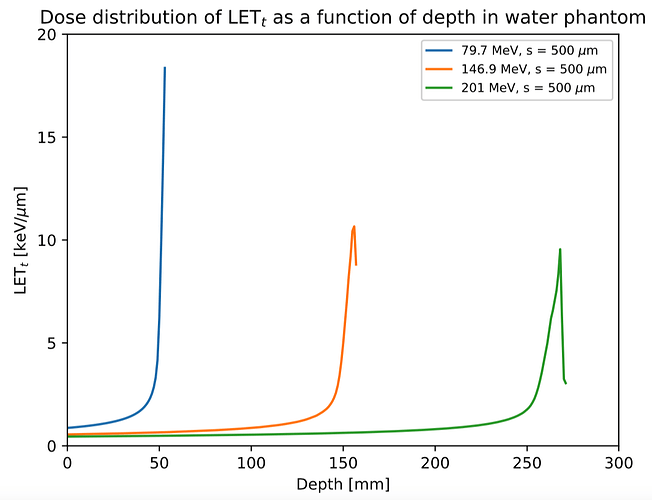
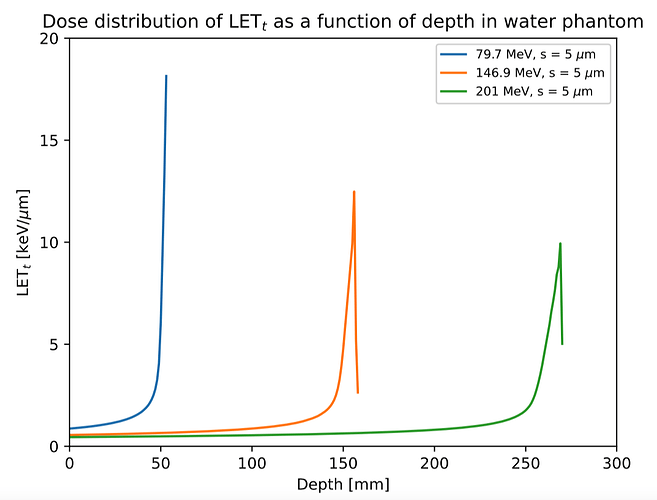
Dear FLUKA experts,

I’d like to score both LETd and LETt of primary protons in water.
I tried to use GETLET routine in fluscw.f and comscw.f.
And the results seem incorrect and they highly depend on the proton beam shape. (In principle they should not.)
My procedures are:

  1. define 4 USRBINs to score LETd (dose, 21bin), dose (22 bin), LETt (fluence, 23 bin), fluence (24 bin)
  2. use USERWEIG to link fluscw.f and comscw.f
  3. in both fluscw.f and comscw.f, I set (JTRACK.EQ.1 .AND. LTRACK.EQ.1) to score only primary protons and use GETLET function, else FLUSCW or COMSCW will be ZERZER
  4. link 21bin to comscw.f and link 23bin to fluscw
  5. when the simulations are done, the final voxel by voxel LETd should be (21 bin)/(22 bin), and LETt should be (23 bin)/(24 bin).

I’m not sure whether my understanding is correct.
I have attached the inp and two .f files.

And one more question, for the ENDLET and BEGLET, which one should I use in my case?

Thank you very much!
protonPeak.inp (1.5 KB)
fluscw_proton.f (5.2 KB)
comscw_proton.f (6.0 KB)

3

Dear @kwlibuaa,

Thank you for your question. First of all, would you mind sharing some of the results that you find incorrect, together with the beam shape dependance? It would be very useful to me in order to pinpoint the differences.

Using as a reference this post with the canonical definition of LETt and LETd, it seems to me that your LETt calculation is coherent. However, the way you define LETd is different since dose is used, which is proportional to the deposited energy. You are somehow combining the second and third definitions in the post. Possibly your definition and the canonical one may coincide under certain conditions, but formally speaking they are different. I propose you use the following:

21bin - Proton fluence,
22bin - Proton fluence weighted by LET via fluscw,
23bin - Proton fluence weighted by LET^2 via fluscw,

Hence: LETt = 22bin/21bin ---- LETd = 23bin/22bin.

Lastly, I understand you ask about using either the initial or final LET for each step in the USRBIN calculations. In general, using the initial values of the particle (ETRACK and PLA) in each step for GETLET yields accurate results. In your code, this is obtained via:

ENDLET = GETLET(JTRACK,EKIN,PLA,ZERZER,26)

Please remember that the accesible values in the variables are always the initial ones, which are used to determine the values of the next step. Also, take into account that depending on the voxel size of USRBIN, more than one particle step can take place inside. In such case, fluence values with their weights are properly averaged.

I hope this helps.

Mario Sacristán Barbero

1 Like
4

Dear Mario,

Thanks a lot for your reply!

I followed your answer to set the .inp file and fluscw.f file.
The results seem to be correct. But still there was a dropping tail at the end of the depth-LET line. As a showed in the following.

But another question occurs. I tried to simulate the primary proton LET with different step length limit. I tested the maximum step lengths of 5mu and 500mu. In principle, the LETt should be the same for LETt, and the LETd should be different. But my results seem that both LETt and LETd are almost the same. I don not know why.

image
image1084×821 61.2 KB

image
image1074×821 60.1 KB

image
image1057×810 58.8 KB

image
image1075×817 58.3 KB

image
image1178×502 107 KB

The last figure was adapted from a reference simulated by Geant4. I’d like to reproduce those results by FLUKA.

And the following are the files that I used.
fluscw_proton.f (5.9 KB)
protonPeak.inp (1.3 KB)

1 Like
5

Dear @kwlibuaa,

Thank you again for your message.

The decreasing tail at the end of the LETt and LETd vs depth is the combination of the unresolved drop after the Bragg peak and the effect that, at the end of the curve where the fluence drops, numerical problems may emerge due 1/0 behaviour (also discussed in the post).

Related to the results from G4 you intend to reproduce, I understand they come from the following article: https://aapm.onlinelibrary.wiley.com/doi/epdf/10.1118/1.4932217.

In the figure 1 of that article, it is explained how fluence, LET and deposited energy are scored. Essentially, fluence and energy are scored in the thickness-dependant front layer of every voxel, while the deposited energy is calculated in the whole voxel. On the contrary, in your FLUKA input file, every variable is scored and averaged in the whole voxel. In particular, your simulation matches the case of 500um step thickness in G4 since the voxel size is 500um as well.

Related to your last comment:

In the section 3.B of the article, the author comments on the higher LETd values found for the case of 5um, which seem to appear due to small step sizes and disappear for larger steps. In FLUKA, the role of the step size is the same as for the large steps in the article. This is why all of your results are identical among them in FLUKA (step-size independent), and equivalent to those of 500 um in G4.

If you want to implement the alternative scoring methodology in FLUKA, you would need to have different USRBIN grids to score fluence, energy and deposited energy.

I hope this is helpful.
Best regards,

Mario Sacristan Barbero

1 Like
6

Dear Mario,

Thank you very much for your detailed explanation!
Now it is very clear for me!

Best regards,
Kaiwen